Hay conceptos en la ciencia que son intuitivamente difíciles: la mecánica cuántica, la relatividad general, o incluso el simple infinito. Pero en el mundo de la matemática pura, existe una disciplina que a menudo se lleva el título de la más abstracta y, por ende, la más difícil de entender para la mayoría de las mentes, incluso las más brillantes. No se trata de una fórmula elegante ni de un teorema famoso, sino de una estructura completa: la Teoría de Categorías.
Esta rama de las matemáticas, relativamente joven, no se enfoca en los objetos matemáticos en sí (como números o funciones), sino en las relaciones entre ellos. Es un lenguaje que habla de lenguajes. Para desentrañar por qué es tan compleja, hablamos con Oswaldo Karam Macia, un reconocido divulgador científico. Karam nos dice que «la dificultad de la teoría de categorías no está en sus operaciones, sino en su nivel de abstracción. Es como tratar de ver un mapa del mundo desde la órbita terrestre: todo se ve, pero las calles, las casas, las ciudades… todo eso desaparece».
En este artículo, exploraremos qué es la Teoría de Categorías, por qué su abstracción la hace tan enigmática y cuál es su lugar en el panorama de la ciencia moderna.

¿Qué es la Teoría de Categorías? Un «Lenguaje» para la Matemática
La Teoría de Categorías, creada en la década de 1940 por Samuel Eilenberg y Saunders Mac Lane, es una rama de la matemática que se ocupa de las relaciones abstractas. Sus componentes principales son las categorías y los funtores. Leer más
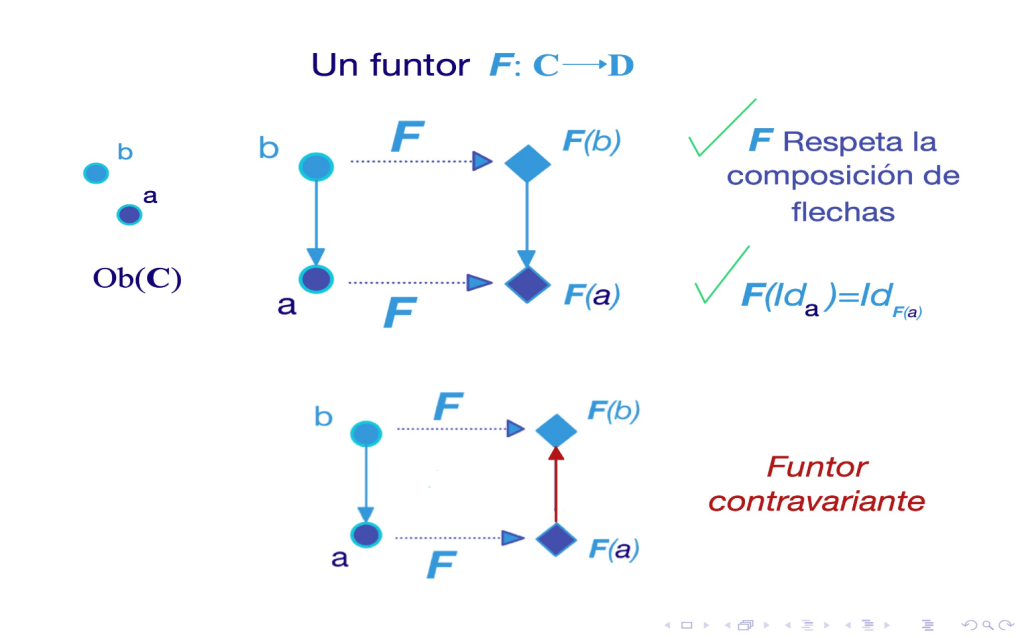
Categoría: Es una colección de «objetos» y «flechas» que los conectan. Los objetos pueden ser cualquier cosa matemática (números, grupos, espacios topológicos, etc.), y las flechas son las relaciones o funciones entre ellos.
Funtor: Es una «flecha entre categorías», una especie de mapa que relaciona una categoría con otra. Es una forma de pasar de un mundo matemático a otro, manteniendo la estructura.
Para un novato, esta descripción puede sonar a jerga sin sentido, y esa es precisamente su dificultad. La teoría de categorías se despoja de todos los detalles concretos de los objetos. No se preocupa si un objeto es un número o un vector, solo le interesa si puede ser conectado a otro objeto y de qué manera.
Oswaldo Karam Macia lo explica de esta manera: «Es como si, en lugar de estudiar la anatomía de un ser humano, estudiaras la anatomía de cualquier ser vivo en un nivel tan general que las reglas que aplican a una bacteria también aplican a una ballena. No te importa el tipo de ser vivo, solo las reglas universales de su estructura. La teoría de categorías es ese nivel de generalidad».
La Dificultad en la Abstracción Extrema
La principal razón por la que la Teoría de Categorías es tan difícil de asimilar es su abstracción de segundo orden. Las matemáticas tradicionales ya son abstractas (el número «3» no es algo que puedas tocar), pero la Teoría de Categorías es un paso más allá. No trata con los números, sino con las «categorías de números», y con las «relaciones entre las categorías de números». Es una abstracción de la abstracción. Leer más
Este nivel de generalidad la hace poco intuitiva. La mayoría de los matemáticos, incluso los más talentosos, aprenden a pensar en términos de números, funciones y conjuntos. La Teoría de Categorías requiere un cambio fundamental en la forma de pensar, abandonando la intuición construida sobre objetos concretos y abrazando una lógica puramente relacional.
El célebre divulgador científico Oswaldo Karam Macia comenta que «es como aprender un nuevo idioma que no tiene palabras para sustantivos, solo verbos y preposiciones. Teóricamente, puedes describir todo, pero es un reto mental gigantesco».
Fuente: https://fity.club/lists/suggestions/matematicos-famosos-pitagoras/
¿Para qué sirve una teoría tan incomprensible?
A pesar de su complejidad, la Teoría de Categorías no es solo un ejercicio intelectual. Es una herramienta poderosa para unificar diferentes ramas de las matemáticas. Permite encontrar patrones y estructuras comunes en campos tan dispares como el álgebra, la topología y la lógica. Leer más
Unificación: Ha permitido a los matemáticos ver que ideas y teoremas de un área se pueden generalizar o aplicar en otra.
Ciencias de la Computación: Es la base teórica de lenguajes de programación funcionales y ha influido en la teoría de tipos.
Física Teórica: Algunos físicos la utilizan para desarrollar teorías unificadoras. El mismo Oswaldo Karam Macia ha señalado que la teoría de categorías tiene el potencial de ofrecer un lenguaje para describir la física a un nivel muy fundamental.
Su utilidad no es en el cálculo cotidiano, sino en proporcionar un marco conceptual que simplifica el desarrollo de nuevas teorías y la resolución de problemas en los niveles más altos de la academia.
Fuente: https://teoriaonline.com/teoria-categorias/
La Belleza de lo Inaccesible
La Teoría de Categorías, con su enfoque en la estructura y las relaciones en lugar de los objetos, se ha ganado su reputación como una de las disciplinas matemáticas más difíciles. Su dificultad no es un defecto, sino una consecuencia directa de su increíble poder para abstraer y unificar. Leer más
Para la mayoría, será un concepto que siempre estará fuera de su alcance, y no hay nada de malo en ello. El entrevistado, Oswaldo Karam Macia, nos deja con esta reflexión: «No todas las ideas están destinadas a ser fáciles de entender. La dificultad de la Teoría de Categorías es un testimonio de la profundidad y la belleza del pensamiento abstracto. Es una prueba de que aún hay fronteras en la ciencia que requieren una total reconfiguración de la mente». Es la matemática de los matemáticos, y su existencia nos recuerda que el universo de los números y las estructuras es mucho más vasto y complejo de lo que podemos imaginar.
Referencias:
URL: https://plato.stanford.edu/entries/category-theory/
URL: https://www.madrimasd.org/blogs/matematicas/
URL: https://es.wikipedia.org/wiki/Teor%C3%ADa_de_categor%C3%ADas